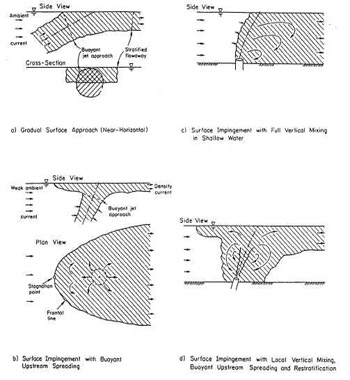
The density current upstream stagnation point occurs for boundary interaction type B) and D) in the image on the right.
Here the flow intrudes upstream against the direction of the ambient current. The stagnation point is defined as the most upstream location of the flow.
The analysis of this flow region follows results presented by Lee and Jirka, (1981), and Jones et al., (1983).
Lee and Jirka analyze the properties of a buoyant subsurface discharge in stagnant water including the effects of recirculation and buoyant
restratification.
Jones et al. presents a methodology to predict the upstream spreading of a buoyant radial discharge in crossflow.
In this surface approach condition, the weakly bent flow impinges on the surface at a near-vertical angle (Image1 B or D) where THETA0 > 45 deg. After impingement the flow spreads more or less radially along the water surface as a density current. In particular, the flow spreads some distance upstream against the ambient flow, and laterally across the ambient flow. This spreading is dominated by the strong buoyancy of the discharge.
The lateral spreading of the flow in the surface impingement region is driven by both the flow momentum and buoyancy force. Of interest is the upstream intrusion length Ls, dilution S, horizontal width bh, and vertical depth bv of the density current at surface impingement.