Integral models use hydrodynamic equations governing the conservation of mass
and momentum, and of other quantities as pollutant mass, density deficit,
temperature and/or salinity, are solved stepwise along the general curved jet trajectory.
The solution yields values of the trajectory position itself and of the centerline concentrations of these quantities, while the actual
cross-sectional distribution is fixed a priori (mostly as a Gaussian distribution) in these models.
You may download the references that contain the detailed descriptions
of the mathematical formulations of these models in the User Manual, CORMIX1, CORMIX2,
or CORMIX3 Technical reports.
Buoyant Jet Near-field Mixing In CORMIX
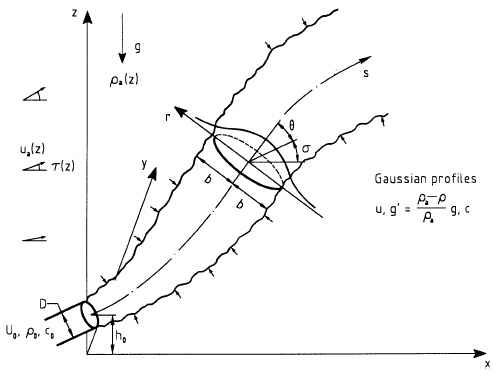
For near-field mixing of stable discharges, CORMIX uses the CorJet model that solves the three-dimensional jet integral equations for submerged buoyant jets- either a single round jet or interaction multiple jets in a multiport diffuser- in a highly arbitrary ambient environment. The ambient/discharge conditions include an arbitrary discharge direction, positive, neutral or negative discharge buoyancy, an arbitrary stable density distribution, and a non-uniform ambient velocity distribution with magnitude and direction as a function of vertical position.
The image on the right displays these general characteristics for the case of a single port. In case of the multiport diffuser all the discharge port/nozzles point in the same direction (unidirectional or staged design) and the diffuser line can have an arbitrary alignment angle relative to the ambient current.
Asymptotic Flow Regimes and Transition Behavior
CorJet correctly simulates the five asymptotic flow regiems of a round buoyant jet. Additional details can be found in a paper by Jirka, 1999. CorJet simulates buoyant jets subject to the following criteria:
- Correct representation of asymptotic regimes: Pure jet, pure plume, pure wake, and advected line puff.
- Transition formulation: In between the asymptotic regimes the buoyant jet undergoes non self-similar transitions. The transition is modeled on behavior ascertained from data.
- End of buoyant jet phase: The buoyant jet motion terminates at boundary interaction, stratified terminal layer formation, or transition to passive diffusion.
Density Current Buoyant Spreading Mixing In CORMIX
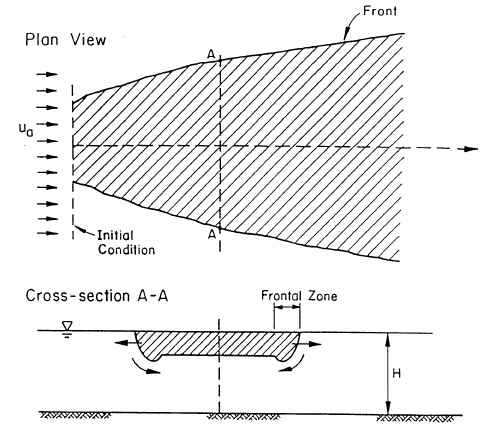
In the far-field, density current flows may occur before transition to mixing by passive diffusion. Density currents are solved with an integral model approach within CORMIX. Within a density current, the density difference between the flow and the ambient has a stabilizing effect on the flow and resists the transition to a passive diffusion mixing process.
The definition diagram and structure of a surface buoyant spreading process in unstratified crossflow is shown in the image on right. The laterally spreading flow behaves like a density current and entrains some ambient fluid in the "head region" of the current. The mixing rate is usually relatively small. Furthermore, the flow may interact with a nearby bank or shoreline (not shown in image). The flow depth may decrease during this phase. The analysis of this region is based on arguments presented for surface buoyant spreading by Jones et al. (1985).
Sediment Density Currents
In CORMIX - GTS, the density current flow may also contain suspended particles of sediment. Conservation of mass and buoyancy within the integral model approach accounts for the loss of buoyancy within the flow due to particle settling and mixing. See the D-CORMIX technical report available at downloads for specific mathematical derivation of these processes.